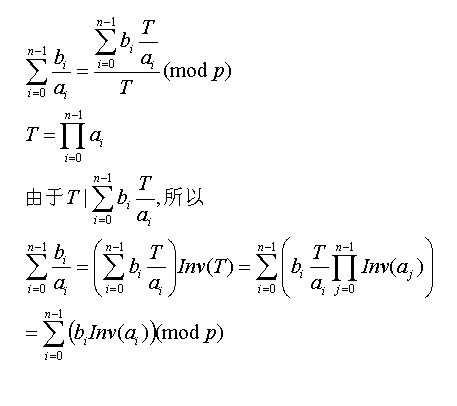
乘法逆元
乘法逆元，是指数学领域群G中任意一个元素a，都在G中有唯一的逆元a‘，具有性质a×a'=a'×a=e，其中e为该群的单位元。
基础资料
简介
定义内容
群G中任意一个元素a，都在G中有唯一的逆元a‘,具有性质
，其中e为群的单位元。举例说明
例如：4关于1模7的乘法逆元为多少？
这个方程等价于求一个X和K，满足
其中X和K都是整数。
若
则称a关于1模f的乘法逆元为x。也可表示为。当a与f互素时，a关于模f的乘法逆元有解。如果不互素，则无解。如果f为素数，则从1到
的任意数都与f互素，即在1到之间都恰好有一个关于模f的乘法逆元。例如，求5关于模14的乘法逆元：
说明5与14互素，存在5关于14的乘法逆元。
因此，5关于模14的乘法逆元为3。
其求法可用欧几里德算法：
Extended Euclid (d，f) //算法求d关于模f的乘法逆元d，即
1.
2.
无逆元3.
为逆元4.
整除5.
6.
7.
8.
常用于加密算法中，如仿射算法。
求此算法还可以使用费马小定理
只不过局限性比较大，要求模数是素数
p要求是素数
那么
就是a的乘法逆元
最新入驻